Построить треугольник. Дополнительная задача 319 § 4 глава 4 Геометрия 7-9 класс Атанасян Л.С.

Вот ответ:

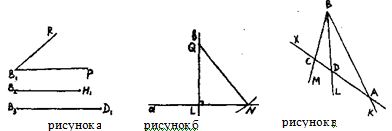
Пусть надо построить ∆АВС, и даны углы RB1Р и отрезки: В2Н1, равный высоте треугольника, B3D1 равный медиане треугольника (см. рис. а). Построим произвольную прямую а, отметим на ней точку L и через точку L проведем прямую в перпендикулярную прямой а (см. пункт 23 учебника). На прямой в от точки L отложим отрезок LQ, равный данному отрезку В2Н. Построим окружность с центром в точке Q и радиусом B3D1, она пересечет прямую а в точке N(см. рис. б). Построим произвольный луч ВМ, отложим от него угол МВК равный данному углу RB1P(см. пункт 23 учебника). Построим биссектрису BL угла МВК, отложим отрезок BD равный данному отрезку B3D1(см. рис. в).От луча DBотложим угол BDX равный углу QNL, луч DX пересечет луч ВМ в точке с. Проведем прямую CD, она пересечет луч ВК в точке А. Треугольник АВС есть искомый.