Построение окружности. Задача 350 § 4 глава 4 Геометрия 7-9 класс Атанасян Л.С.
Лови решение)
Рассмотрим прямоугольный ∆ ВСВ1, с прямым углом ВВ1С (так как ВВ1 - высота ∆ АВС, следовательно, ВВ1 перпендикулярна АС).
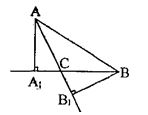
В прямоугольном треугольнике гипотенуза больше катета, т.е.
ВС ≥ВВ1, учитывая, что по условию АА1≥ВС, получаем
АА1≥ВС≥ВВ1. Рассмотрим прямоугольный ∆АСА1 с прямым уг-
лом АА1С (т.к. АА1 - высота ∆ АВС, следовательно, А1 перпенди-
кулярна ВС). В прямоугольном треугольнике гипотенуза больше ка-
тета, т.е. АС≥АА1, учитывая, что по условию ВВ1≥АС, получаем
ВВ1≥АС≥АА1, по доказанному АА1≥ВС≥ВВ1 следовательно,
АА1=ВВ1.
ВВ1=АА1≥ВС≥ВВ1, следовательно, ВС=ВВ1 и ∆ВСВ1 равнобед-
ренный, а углы при основании равнобедренного треугольника рав-
ны, следовательно,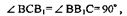 
тогда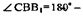 
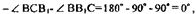следовательно, ВВ| совпадает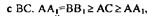 
следовательно, АС=А1 и ∆ АСА1 равнобедренный, а углы при основании равнобедренного треугольника равны следовательно
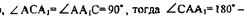
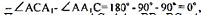значит, АА1 совпадает с АС.
По доказанному АС=АА1=ВВ1=ВС и АС перпендикулярны ВС, сле-
довательно, А АВС - равнобедренный и прямоугольный, что и тре-
бовалось доказать.
