Построение биссектрисы угла. Дополнительная задача 175 § 4 II глава Геометрия 7-9 класс Атанасян Л.С.
Ребята, привет, помогите разобраться с построением биссектрисы угла?
На сторонах угла XOY отмечены точки А, В, С и Dтак, что ОА = ОВ, AC = BD (рис. 97). Прямые ADи ВС пересекаются в точке Е. Докажите, что луч ОЕ — биссектриса угла XOY. Опишите способ построения биссектрисы угла, основанный на этом факте.
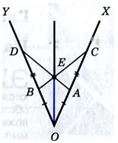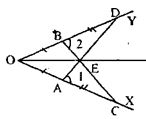
Дано: ОА=ОВ, АО=ВD
Доказать: ОЕ — биссектриса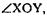 
Доказательство:
Рассмотрим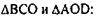 
угол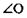 
— общий, ОА=ОВ, ОD=ОС
(т.к. ОD=ОВ+ВD=OА+АC=ОС) значит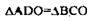 
по 1-му признаку следовательно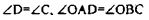 
следовательно, DЕ=ЕС.
Рассмотрим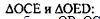 
сторона ОЕ — общая, OD=ОС, DЕ=ЕС, значит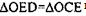 
по 3-му признаку, следовательно, 
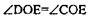и значит ОЕ — биссектриса
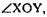что и требовалось доказать.
Описание способа построения биссектрисы угла, используя эту за-
дачу:
1) построить окружность с центром в вершине угла любого радиуса. Окружность пересечет стороны угла в точках А и В.
2) построить окружности с центрами в точках А и В одинакового радиуса. Окружность с центром А и радиусом R. пересечет сторону угла в точке С, также окружность с центром В и радиусом R пересечет сторону угла в точке D. Значит:
3) Построим отрезки АD и ВС.
4) Они пересекутся в точке Е.
5) Соединим лучом вершину угла и точку Е. Полученный луч и
будет биссектрисой.
