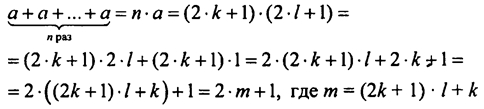Помогите доказать про сумму чисел. № 630. ГДЗ Математика 5 класс Никольский.

а) Пусть n нечетных слагаемых а, где n — четное число, т.е.
n представляется в виде n=2 ∙ k, где k — некоторое натуральное число. Покажем, что сумма четного числа нечетных слагаемых четная.

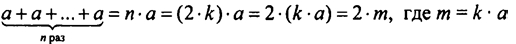
Таким образом, сумма представляется в виде 2 ∙ m, где m — некоторое натуральное число, т.е. сумма четного числа нечетных слагаемых
четная.
б)   Пусть имеется п нечетных слагаемых а, где n — нечетное число,
т.е. а и n представляются в виде а = 2∙ l+1, n = 2∙k+1, где k, l —
некоторые натуральные числа.
Покажем, что сумма нечетного числа нечетных слагаемых нечетная.
 
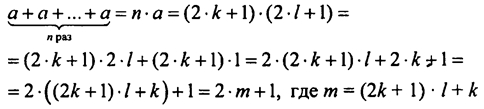
Таким образом, сумма представляется в виде 2∙m+4, где m — некоторое натуральное число, т.е. сумма нечетного числа нечетных слагаемых нечетная.