Помогите №49 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Докажите, что если луч, исходящий из вершины угла, пересекает отрезок АВ с концами на сторонах угла, то он пересекает
1) отрезок АС с концами на сторонах угла;
2) любой отрезок СD с концами на сторонах угла.

1 ответ

ответы

Оксана Кустова

Пожаловаться

1) Пусть К — точка пересечения луча с отрезком АВ. Прямая ОК пересекает отрезок АВ, следовательно, точки А и В лежат в разных полуплоскостях относительно прямой ОК. Точки В и С лежат в одной полуплоскости, так как отрезок ВС не пересекается с прямой ОК, а точки А и С лежат в разных полуплоскостях, получаем, что прямая ОК пересекает отрезок АС в некоторой точке, обозначим ее буквой Е.
Прямая ВС разбивает плоскость на две полуплоскости, в одной из которых лежит данный луч ОК и точка А (поскольку отрезок АК не пересекает прямую ОB) и точка Е (поскольку отрезок АЕ не пересекает прямую ОB). Значит, точка Е должна лежать на луче ОК.

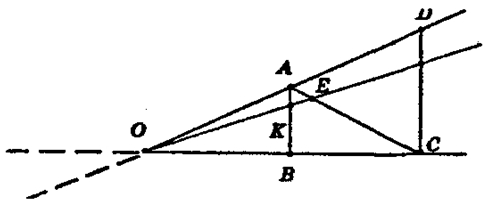
1) Пусть СD — произвольный отрезок с концами на сторонах угла, и точка С лежит на стороне ОВ, а точка D на стороне ОА. Отрезок АВ пересекает луч ОК, значит, луч ОК пересекает и отрезок АС, а если луч пересекает АС, то луч будет пересекать и отрезок СD.
Что и требовалось доказать.