Периметр треугольника. Задача 345 § 4 глава 4 Геометрия 7-9 класс Атанасян Л.С.

Ребя, а кто имел дело с периметром треугольника?
Через вершину А треугольника АВС проведена прямая, перпендикулярная к биссектрисе угла А, а из вершины В проведён перпендикуляр ВН к этой прямой. Докажите, что периметр треугольника ВСН больше периметра треугольника АВС.

1 ответ

ответы

Никита Рыжков

Пожаловаться

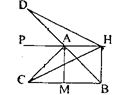
Продолжим отрезок ВА на отрезок АD=АС. Пусть АМ - биссектриса угла САВ, следовательно, 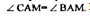 По условию прямая РА перпендикулярна биссектрисе АМ (см. рисунок).,

следовательно,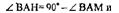

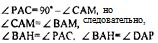
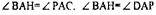  как вертикальные, значит,

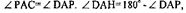
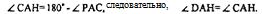
∆ САН= ∆DАН (по двум сторонам и углу между ними: СА=АD по
построению, АН — общая сторона, 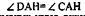 (по доказанному
му). В равных треугольниках против равных углов лежат равные
стороны, значит, СН=DН. Из неравенства треугольника следует, что DН=НВ>DВ, но DВ=DА+АВ=СА+АВ. По доказанному DН=СН,
следовательно, СН+НВ>СА+АВ.
У треугольников ВСН и АВС сторона СВ - общая. Р ∆BCH =СН+НВ+СВ; Р∆ABC =СА+АВ+СВ, из того, что СН+НВ>СА+АВ следует, что Р ∆BCH>Р ∆ABC. Что и требовалось доказать.