Найдите углы §6 №64 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Меньшее основание равнобокой трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне Найдите углы трапеции.

1 ответ

ответы

Аза Алиева

Пожаловаться

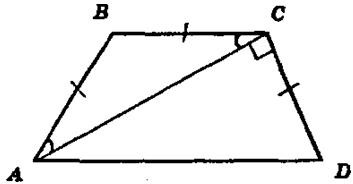
Рассмотрим ΔАВС:
АВ = ВС, значит, ΔАВС равнобедренный и ∠BAC = ∠BCA Пусть ∠BAC = ∠BCA = х°.
Но ∠CAD = ∠ACB (как накрест лежащие при параллельных прямых AD и ВС и секущей АС). Значит ∠CAD = х° Значит, АС
— биссектриса угла BAD. В равнобокой трапеции углы при основании равны, тогда ∠D = ∠BAD = 2х°.
Рассмотрим ΔACD:
∠CAD = х°; ∠D = 2х°; ∠ACD = 90°.
Составим уравнение: х + 2х + 90 = 180; откуда получим 3х = 90; х = 30, то есть
∠BAC = 30°; ∠BAD = ∠CDA = 2 · ∠ВАС = 2·30° = 60°.
∠ABC = ∠BCD = ∠ACB + ∠ ACD = 30° + 90° = 120°.
Ответ: 60°; 60°; 120°; 120°.