Найдите стороны прямоугольника §6 №45 ГДЗ Геометрия 7-9 класс Погорелов А.В.

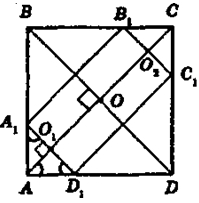
∠BOA = 90° (диагонали квадрата пе-
ресекаются под прямым углом)
∠BOA = ∠A₁O₁A = 90° (как соответ-
ственные углы для параллельных пря-
мых BD и A₁D, и секущей АС)
АС — биссектриса, поэтому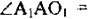 
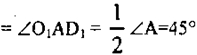
Значит, ∠AA₁O₁ = ∠AD₁O₁ = 45°
ΔA₁AD₁ — равнобедренный; так как АО1 является высотой, бис-
сектрисой, а значит и медианой. Значит А₁O₁ = O₁D₁ ΔAO₁D₁ —
равнобедренный, значит, A₁O₁ = O₁D₁. Так что, A₁O₁=AO₁=A₁D₁. Пусть отрезок A₁O₁=x м, тогда A₁D₁=2x м и A₁B₁=2A₁D₁=4 м. Далее, AC=AO₁ + O₁O₂ + О₂С=АО₁ + A₁B₁ + O₂С, х+4х+х= 12; 6х = 12 м; х = 2 м. Тогда A₁D₁ = 2х = 2·2 м = 4 м;
А₁В₁=4х = 8м.
A₁D₁ = В₁C₁ = 4 м; A₁B₁ = D₁C₁ = 8 м.
Ответ: 4 м; 8 м.