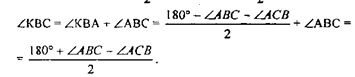Найдите стороны четырёхугольника. Задача 362 § 1 глава 5 Геометрия 7-9 класс Атанасян Л.С.
Привет, вот решение
Пусть надо построить ∆АВС и даны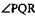 
стороне треугольника, и МN, равный сумме двух других сторон
треугольника (см. рис. а). Проведем произвольную прямую а, отме
тим на ней точку В и точку X (см. рис. б). От луча ВХ отложим угол
ХВL равный углу РQR (см. пункт 23 учебника). От точки В отло-
жим отрезок ВС, равный данному отрезку В1С1. Построим биссек-
трису ВК угла LВС (см. пункт 23 учебника). Построим окружность
С радиусом равным МN и центром в точке С, она пересечет луч ВК
в точке О. Отложим от луча ВК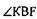 
пересечет СО в точке А. Треугольник АВС есть искомый, докажем это.
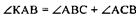(как внешний)
ДКАВ равнобедренный (т.к.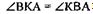 
по построению), значит
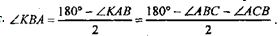
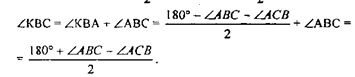
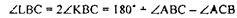(так как ВК — биссектриса угла LВС).
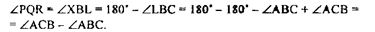
АВ = АК, так как ∆КВА равнобедренный, значит, МN = КА + АС = = АВ + АС следовательно наши построения верны.
