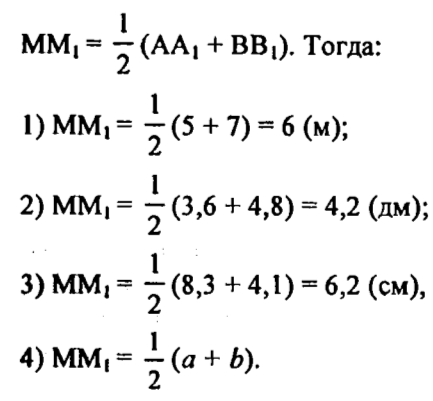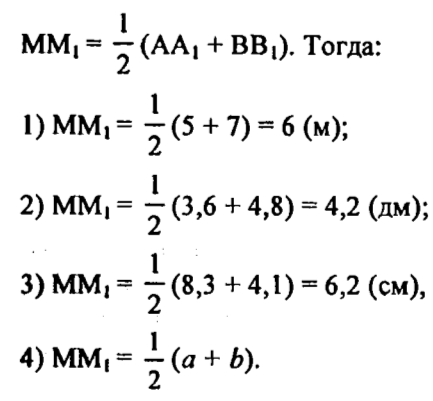Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость.ГДЗ. Геометрия. 10 класс. Погорелов. § 2 п.7 Задача 5

Лови ответ. Опираясь на доказательство следующее доказательство:

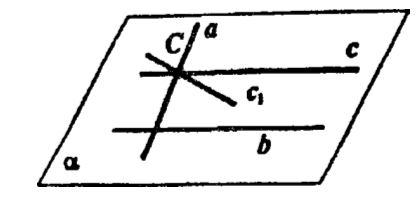
Пусть с — произвольная прямая, параллельная прямой b, пересекающая прямую а. Прямые а и b образуют плоскость а. Проведем через точку С пересечения прямых а и с в плоскости а прямую с1, параллельную b. По теореме 2.1 через точку С можно провести только одну прямую, параллельную b. А, значит, прямая с совпадает с прямой с1, а, значит, принадлежит плоскости α.
Итак, любая прямая с, параллельная b и пересекающая прямую а,
лежит в плоскости а. 
Таким образом, прямые АА1, ММ1, ВВ1, лежат в одной плоскости β.
 
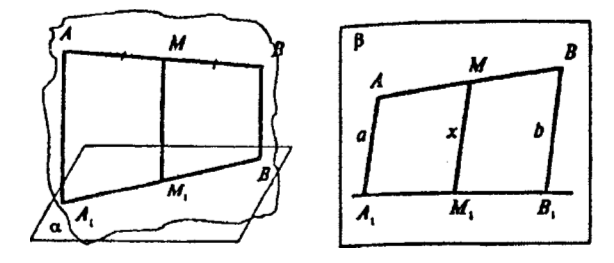
Значит точки А1, В1 и М1 лежат на прямой А1В1 пересечения
плоскостей α и β. Рассмотрим далее картинку в плоскости β. По
теореме Фалеса М1 середина отрезка А1В1. А, значит, ММ1 — средняя линия трапеции АА1В1В и по теореме о средней линии: