Любая плоскость, параллельная прямым АВ и CD,пересекает прямые АС, AD, BDи ВС в вершинах. ГДЗ. Геометрия. 10 класс. Погорелов. § 2 п.10 Задача 22

 

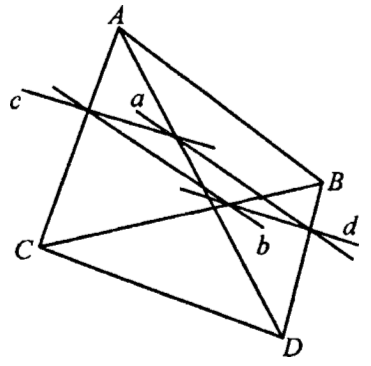
Допустим некоторая плоскость α параллельна прямым АВ и CD.
Согласно утверждению: если плоскость β, проходит через прямую а, параллельную другой плоскости α, и пересекает эту плоскость по второй прямой b, то прямые а и b параллельны. Из параллельности прямой АВ и плоскости а следует, что плоскости
определенные тремя точками АВС и ABD пересекают плоскость а  по прямым а и b, параллельным прямой АВ. Из теоремы 2.2 следует, что прямые а и b параллельны.
Из параллельности прямой CD и плоскости а следует, что плоскости ACD и BCD пересекают плоскость а прямым с и d параллельным прямой CD, а, значит, c\\d. Каждая из точек пересечения плоскости а с прямыми АС, AD, BD, ВС лежат в плоскости а и является точкой пересечения каких-то двух не параллельных из прямых а, b, с, d. Например, точка пересечения прямой АС с плоскостью а принадлежит плоскостям АВС и ACD, а значит является точкой пересечения прямых b ис, где b ис — прямые пересечения плоскости а с плоскостями АВС и ACD соответственно.
Так как прямые а и b, с и d попарно параллельны, то построенная
по условию задачи фигура есть параллелограмм. Что и требовалось доказать.