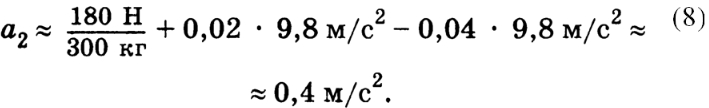Какую скорость приобрел № 291 ГДЗ Рфизика 10 класс Рымкевич А.П.

Уравнение движения мотоцикла на гори-
зонтальном участке дороги
ma1 = F - μmg, (1)
v1 = at. (2)
Здесь а1и v1 — проекции ускорения и скорости на на-
правление движения, F — сила тяги, μ — коэффици-
ент сопротивления, m — масса мотоцикла. Из усло-
вия задачи находим ускорение на горизонтальном
участке дороги:

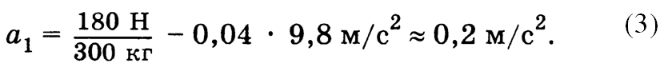
Следовательно, за половину общего времени движе-
ния, т. е. за 5 с, мотоцикл набрал скорость
 
v1 = 0,2 м/с ∙ 5с² = 1 м/с. (4)
На наклонном участке дороги движение мотоцикла
определяется двумя проекциями векторного уравне-
ния динамики — на направление, перпендикулярное
наклонной плоскости:
0 = N - mg cos α, (5)
и направление движения мотоцикла:
mа² = F + mg sin α - μN. (6)
Здесь α — угол наклона дороги к горизонту, N — сила
реакции опоры (дороги), α — ускорение на втором
участке движения. Исключая из уравнений (5), (6)
силу N, получаем ускорение
Подставляя в эту формулу данные задачи, находим
ускорение мотоцикла на наклонном участке дороги:

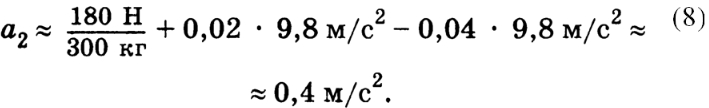
Уравнение для изменения скорости на этом участке
имеет вид
v2 = vl + a2t (9)
где — скорость, набранная на горизонтальном уча-
стке. Подставляя в уравнение (9) величины v1 и а2 из
формул (4) и (8), находим скорость, набранную за 10 с:
v2 = 1 м/с + 0,4 м/с² ∙ 5 с = 3 м/с.
Ответ: v2 = 3 м/с.