ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №673. постройте касательную, проходящую через ...

 Решение задачи Гл.VIII №673 очень простое.

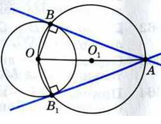
Пусть даны окружность с центром О и точка А вне этой окружности. Допустим, что задача решена и АВ — искомая касательная. Так как прямая АВ перпендикулярна к радиусу ОВ, то решение задачи сводится к построению точки В окружности, для которой угол ABO прямой. Эту точку можно построить следующим образом: проводим отрезок ОА и строим его середину О₁. Затем проводим окружность с центром в точке О₁ радиуса О₁А. Эта окружность пересекает данную окружность в двух точках: В и В₁. Прямые АВ и АВ₁ — искомые касательные, так как АВ┴ОВ и АВ₁ ┴ОВ1. Действительно, углы АВО и АВ1O, вписанные в окружность с центром О₁, опираются на полуокружности, поэтому они прямые. Очевидно, задача имеет два решения.