Докажите, что прямые пересекаются в одной точке. ГДЗ. Геометрия. 10 класс. Погорелов. § 2 п.8 Задача 12
Лови решение.
Пусть ABCD— данный пространственный четырехугольник
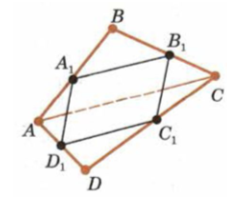
Пусть A1, B1, С1, D1— середины его сторон. Тогда А1В1 — средняя линия треугольника АВС, параллельная стороне
АС,C1D1— средняя линия треугольника ACD,тоже параллельная стороне АС. По теореме 2.2 прямые А1В1 и C1D1параллельны, а значит, лежат в одной плоскости. Точно так же доказывается па-
раллельность прямых A1D1и В1С1. Итак, четырехугольник A1B1C1D1лежит в одной плоскости и его противолежащие стороны параллельны. Следовательно, он параллелограмм.
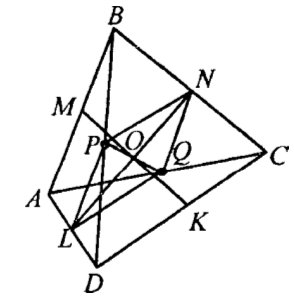
Пусть точки М, N, К, L, P, Q — середины отрезков АВ, ВС, CD, AD, BD, АС соответственно.
Исходя из доказательства описанного выше. Отрезки МК и NL являются диагоналями параллелограмма MNKL с вершинами в серединах сторон четырехугольника ABCD. Значит, МК и NL пересекаются в некоторой точке О и делятся этой точкой пополам. Также отрезки PQ и NL являются диагоналями параллелограмма PNQL с вершинами в серединах сторон четырехугольника ABCD, образованного этими сторонами. Значит, PQ и NL пересекаются и в точке пересечения делятся пополам, а так как О — середина NL, то, значит, О — середина PQ. И PQ и NL пересекаются в точке О. Так что искомые прямые МК, NL и PQ, соединяющие середины отрезков АВ и CD, ВС и AD, АС и BD соответственно пересекаются в одной точке О, что и требовалось доказать.
