Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую. ГДЗ. Геометрия. 10 класс. Погорелов. § 1 п.2 Задача 8

Лови доказательство.

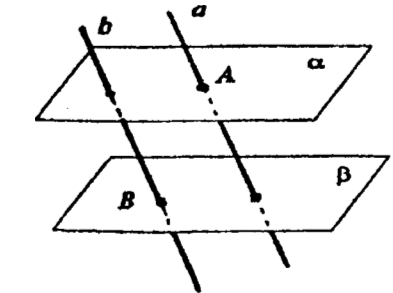
Через произвольную точку В плоскости β проведем прямую b
параллельно прямой а. Так как прямая а пересекает плоскость а, то
параллельная ей прямая b пересекает эту плоскость.
Если плоскость пересекает одну из двух параллельных прямых, то она пересекает и другую, исходя из доказательства, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.
Т.е., так как данные прямые а и b параллельны, то через них можно провести плоскость. Обозначим ее а.
Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью α две общие точки — точки пересечения с данными прямыми. По теореме 1.2 эта прямая лежит в плоскости а.
Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости а.
В нашем случае, а b пересекает плоскость β. Значит, прямая а пересекает плоскость β. Что и требовалось доказать.