Докажите, что преобразование симметрии относительно плоскости есть движение. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.28 Задача 20

Лови доказательство.

Возьмем произвольный отрезок АВ и рассмотрим преобразование
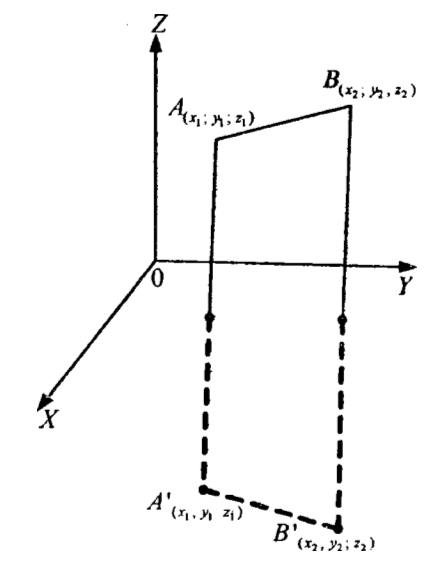
симметрии этого отрезка относительно произвольной плоскости а. Введем декартову систему координат так, чтобы оси х и у лежали в плоскости а. Тогда во введенной системе координат концы отрезка АВ имеют координаты A(x1;y1;z1) и В(x2;y2;z2) а значит, при симметрии они перейдут в точки Α'(x1;y1;-z1) и В(x2;y2;-z2).
В соответствии с доказательством, что преобразование симметрии относительно координатной плоскости хузадается формулами х' = х,у' = у, z' = -z. 
Точка А симметрична точке А'.
Значит эти точки лежат на прямой, перпендикулярной плоскости
ху, находятся по разные стороны от плоскости ху и расстояния от А и А' до ху равны. Поэтому координаты х = х'; у = у' и |z| = = |z'|. А так как А и А' по разные стороны относительно ху, то z' = -z. Следовательно, = х,у' = у, z' = -z. 
Далее: АВ2 = (x1-x2)2+(y1-y2)2+(z1-z2)2;
(A'B')2 = (x1-x2)2+(y1-y2)2+(-z1+z2)2;
(z1-z2)2=(z2-z1)2, так что АВ = А'В', следовательно, это преобразование есть движение.