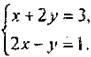Докажите §8 №41 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Найдем точку пересечения прямых х + 2у = 3 и 2х - у = 1. Координаты точки пересечения этих прямых — это решение системы уравнений:

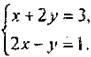
1) х = 3 - 2у подставляем во 2-е уравнение.
2)  2 (3 - 2у) - у = 1; 6 - 4у - у = 1,
5у = 5, у = 1.
3)  x=3-2·1, x=1.
точка пересечения прямых х + 2у = 3 и 2х - у = 1 это (1; 1).
Подставив в уравнение 3х + у = 4 вместо х и у координаты точки (1; 1), получим:
31 + 1 = 4 — верное равенство.
Значит, прямая 3х + у = 4 проходит через точку (1; 1). А значит все три прямые пересекаются в точке (1; 1). Так как никакие две различные прямые не могут иметь более одной общей точки, то (1; 1) — единая общая точка.
Что и требовалось доказать.