Докажите §6 №42 ГДЗ Геометрия 7-9 класс Погорелов А.В.

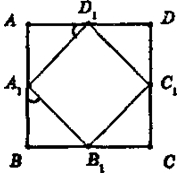
Рассмотрим ΔAD₁A₁, ΔDC₁D₁, ΔСВ₁С₁,
ABA1B1.
AA₁ = DD₁ = CC₁ = BB₁ (по условию). A
значит и AD1 = DC₁ = CB₁ = BA₁.
∠A = ∠D = ∠C = ∠B = 90° (t.k. ABCD
— квадрат). Тогда, ΔAD₁A₁ = ΔDC₁D₁ =
ΔCB₁C₁ = ΔBA₁B₁ (по двум катетам). Зна-
чит, A₁D₁ = D₁C₁ = С₁B₁ = B₁A¹, а также
∠AD₁A₁ = ∠BA₁B₁.
∠AD₁A₁ + ∠AA₁D₁ = 90° (сумма острых углов прямоугольного
треугольника). Значит, ∠BA₁B∠ + ∠AA₁D₁ = 90°. А так как
∠AA₁D₁ + ∠D₁A₁B₁ + ∠BA₁B₁ = 180°, то
∠D₁A₁B₁ = 180°-(∠BA₁B₁+∠AA₁D₁)=90°.
Аналогично доказывается, что и остальные углы четырех-
угольника A₁B₁C₁D₁ прямые. Тогда, данный четырехугольник
A₁B₁C₁D₁ является квадратом. Что и требовалось доказать