Докажите §6 №17 ГДЗ Геометрия 7-9 класс Погорелов А.В.

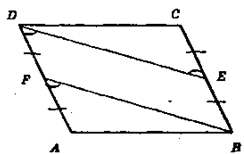
Докажем, что ∠EDF и ∠BFD — односторонние для прямых ED и BF и секущей FD и их сумма равна 180°, а значит, прямая, BF‖ED и, тогда, четырехугольник BEDF— параллелограмм.
Рассмотрим Δ ABF и Δ CDE:
АВ = CD — противоположные стороны параллелограмма.
∠A = ∠C — противоположные углы параллелограмма.
AF= СЕ, так как
Значит, Δ ABF =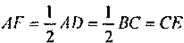 
сторонам и углу между ни-
ми. Следовательно ∠CED=∠AFB. Но ∠CED = ∠EDF (накрест не-
жащие для параллельных ВС и AD и секущей ED). Значит
∠EDF=∠AFB. Поэтому ∠EDF + ∠BFD = ∠AFB + ∠BFD = 180°
так как ZAFB и ZBFD — смежные углы. Тогда, BF||ED и четы-
рехугольник BEDF — параллелограмм. Что и требовалось дока-
зать.