Докажите §5 №15 ГДЗ Геометрия 7-9 класс Погорелов А.В.

1) Через точку А окружности с центром О проведена прямая, не касающаяся окружности. ОВ — перпендикуляр, опущенный на прямую. На продолжении отрезка АВ отложен отрезок ВС = АВ. Докажите, что точка С лежит на окружности.
2) Докажите, что если прямая имеет с окружностью только одну общую точку, то она является касательной к окружности в этой точке.
3) Докажите, что если две окружности имеют только одну общую точку, то они касаются в этой точке.

1 ответ

ответы

Nino Sabidze

дежурный

Пожаловаться

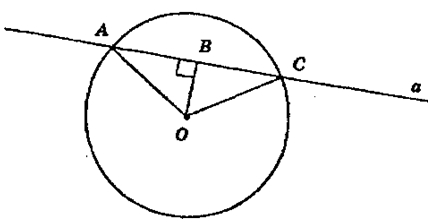
1)       Так как прямая а не касается окружности, то она пересе-
кает окружность в двух точках.
В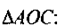
ОВ — медиана (т.к. АВ = ВС (по условию)) и высота (т.к. ОВ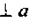
(по условию)). Значит,
разом, ОА = ОС и таким образом точка С принадлежит окружно-
сти.
2)       Пусть прямая а имеет с окружностью только одну общую точку А, но не является касательной, т.е. не перпендикулярна радиусу ОА, таким образом, из точки О можно провести к прямой перпендикуляр ОВ, не совпадающий с ОА. На продолжении отрезка АВ отложим отрезок ВС, равный отрезку АВ. Тогда, из п. 1. точки А и С лежат на окружности. Противоречие, т.к. по условию прямая а имеет с окружностью только одну общую точку.
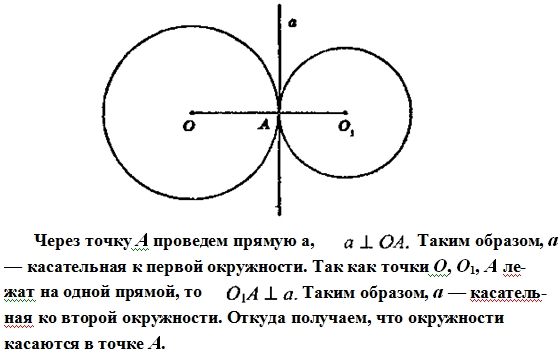
3)       Если две окружности касаются в некоторой точке А, то они имеют общую касательную в этой точке.
Пусть точки О₁, О, А не лежат на одной прямой, тогда имеем ∆ОО₁А. Прямая ОО₁ разбивает плоскость на две полуплоскости,