Докажите §1 №51 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Точки А и В лежат на одной полупрямой с началом в точке С, следовательно, точка С не лежит между точками А и В.
Пусть В лежит между А и С, тогда АС = АВ + СВ и АС > СВ, что противоречит условию: СВ > АС, следовательно, В не лежит между точками А и С.
Из трех точек одна и только одна лежит между двумя другими. На основании предыдущих рассуждений приходим к выводу, что точка A лежит между точками В и С.
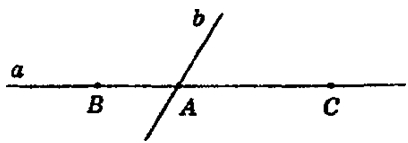
Через точку А проведем прямую b, отличную от прямой а. Точка А лежит между точками B и С, следовательно, отрезок ВС пересекает прямую b, получаем, что точки В и С лежат в разных полуплоскостях относительно прямой b, и по разные стороны от точки А. Все точки прямой а, лежащие в одной полуплоскости с точкой С, расположены по одну сторону от точки А и образуют одну полупрямую АС, а все точки прямой а, расположенные в одной полуплоскости с точкой В, тоже будут лежать по одну сторону от точки А и образуют полупрямую АВ.
Что и требовалось доказать.