Задача №84. Помогите. Сколько плоскостей симметрии...ГДЗ геометрия 11 класс Погорелов

Решение №84
В октаэдре через пару противоположных вершин S₁ и S₂ проходят четыре плоскости симметрии (две из них проходят через ребра A₁S₁, и A₂S₁ а также B₁S₁ и B₂S₁.
Еще две плоскости проходят через ось S₁S₂ перпендикулярно ребрам А₁В₁ и А₂В₁ а также ребрам B₁A₂ и A₂B₂.
 
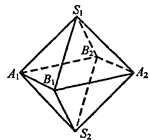
Далее, через пару противоположных вершин A₁ А₂ по тем же со-
ображениям проходят четыре плоскости симметрии; но одна из них,
проходящая через A₁S₁ и A₂S₁ уже была учтена.
Так что есть еще три плоскости симметрии.
Через пару противоположных вершин В₁В₂ проходят также че-
тыре плоскости симметрии, но две из них уже были учтены. Значит,
получим всего 4 + 3 + 2 = 9 плоскостей симметрии.
Правильный икосаэдр имеет 12 вершин.
Через первую пару противоположных вершин проходят пять
плоскостей симметрии (каждая их них проходит через ребро, со-
держащее вершину, перпендикулярно противоположному углу).
Далее, через вторую пару противоположных вершин также про-
ходят 5 плоскостей, но одна из них подсчитана в первом случае, так
что остаются новых четыре плоскости симметрии. 
Для третьей пары получим — 3 новых плоскости, а для четвер-
той — две плоскости и для пятой пары только одна новая плоскость.
Через шестую пару вершин не пройдет ни одной новой плоско-
сти симметрии.
Значит, всего 5 + 4 + 3 + 2 + 1 = 15 плоскостей симметрии.
Правильный додекаэдр состоит из двенадцати правильных пятиуголь-
ников. Так что плоскости симметрии проходят через ребро, содер-
жащее вершину, перпендикулярно противоположному ребру
Поэтому через первую пару противоположных пятиугольников
проходит 5 плоскостей, через вторую пару — 4, через третью — 3,
четвертую — 2, пятую — 1. Так что всего плоскостей симметрии
5+4 + 3 + 2+1 = 15.