Выручайте §9 №36 ГДЗ Геометрия 7-9 класс Погорелов А.В.

У параллелограммов ABCD и A1B1C1D1 АВ = А1В1, AD = A1D1 и ∠A = ∠A1. Докажите, что параллелограммы равны, то есть совмещаются движением.

1 ответ

ответы

Олег Цветков

Пожаловаться

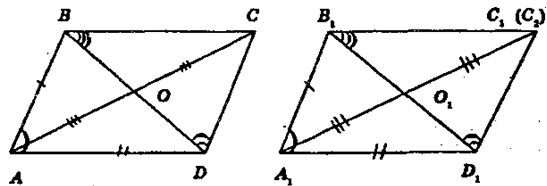
Пусть в параллелограммах ABCD, A1D1C1D1 АВ = A1B1, AD = A1D1, ∠A=∠A1.
Так как ΔABD = ΔA1B1D1 по двум сторонам и углу между ними, то существует движение, переводящее ΔABD в ΔA1B1D1 (см. п. 90). При этом движении луч АО должен совместиться с лучом А1О1 (где О, O1 — точки пересечения диагоналей), так как О и О1 — середины отрезков BD и B1D1 которые при данном движении совмещаются.
При движении сохраняется расстояние между точками, значит, длины АО и А1O1 равны.
АО = ОС и A1O1 = O1C1 (по свойству диагоналей параллелограмма).
Точка С, лежащая на луче АО на расстоянии, равном 2АО от точки А, при данном движении совместится с точкой С2, лежащей на луче А1О1 на расстоянии 2АО от точки А. Точка C1 лежит на луче А1О1 на расстоянии 2A1O1 = 2АО от точки A1 Так как на данном луче от данной точки можно отложить только один отрезок данной длины, то точки С2 и С1 совпадают.
Таким образом, при движении, совмещающем ΔABD с ΔA1B1D1, точки С и C1 тоже совмещаются, а значит, при этом движении параллелограмм ABCD совмещается с параллелограммом A1B1C1D1.