Выручайте §9 №23 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Докажите, что прямая, проходящая через центр окружности, является ее осью симметрии.

1 ответ

ответы

Вадим Ермишен

Пожаловаться

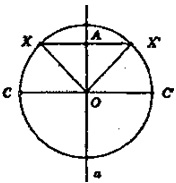
Пусть О — центр окружности, а —
прямая, проходящая через точку О. Пре-
образование симметрии относительно
прямой а переводит точку С окружности
в точку С, а точку О оставляет на месте.
Возьмем произвольную точку X на
окружности и построим точку Х', сим-
метричную точке X относительно пря-
мой а.
ΔOAX = ΔОАХ' так как у них углы при вершине А прямые, сторона ОА — общая, АХ = АХ', так как X и X' - симметричные точки.
Значит ОХ = ОХ', а значит точка X' лежит на окружности. То есть, окружность при симметрии относительна прямой а переходит в себя, так что прямая а - ее ось симметрии.
Что и требовалось доказать.