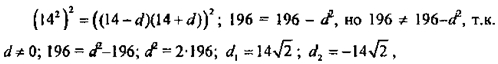Раздел II. № 6.38. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. Помогите разобраться с прогрессиями!

6.38(1) а₁<a₂<а₃ арифметическая прогрессия: а₂-d; a₂; a₂+ d;  d≠0.
Тогда ее сумма 3а₂ = 42; а₂ = 14.
(14-d)²; 14²; (14+d)² – геометрическая гфогрессия; по свойству
членов геометрической прогрессии а²_n = а_n-1 ∙ a_n+1, следовательно
 
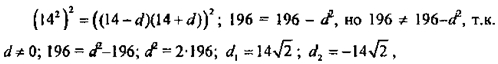
d₂ не удовлетворяет условию задачи, т.к. прогрессия возрастает. Следовательно d = 14√2 .
Ответ: 14-14√2;14; 14+14√2.
 
 
6.38(2) а₁>а₂>а₃ – арифметическая прогрессия;
а₂₁; а₂₂;  а₂₃ – геометрическая прогрессия.
Запишем данные числа в виде: a₂-d; а₂; a₂+d; d ≠ 0; по условию
S₃ = 36; 3а₂ = 36; а₂ = 12; (12-d)²; 12²; (12+d)² — геометрическая прогрессия; 144² = ((12 – d)(12 + d))2; 144 = 144 – d² или 144 = d² – 144;
но 144 ≠ 144 – d², d ≠ 0, поэтому 144 = d²-144; d² = 2∙144; d₁ =12√2
или d₂ = -12√2 . d₁ не удовлетворяет условию задачи, т.к. прогрессия убывает.
Ответ: 12 + 12√2 ; 12; 12 -12√2 .