Раздел II. № 6.29. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. Помогите решить уравнение.

Решите уравнение:
1) (x + 1) + (х + 5) + (x + 9) +...+ (х + 157) = 3200;

2) (x + 248) + (х + 243) + (x + 238) +...+ (х + 3) = 6225.

1 ответ

ответы

Антоша Антонов

Пожаловаться

6.29(1) (x+1)+(x+5)+(x+9)+…+(x+157) = 3200;
x+1; x+5; x+157 - арифметическая прогрессия, т.к. (x + 5)-(x + 1) = 4 и (x + 9)-(x + 5) = 4.
Далее: x + 157 = (x + 1) + 4 ∙ 39. Следовательно x + 157 – 40-й
член этой прогрессии; d = 4. Левая часть уравнения – сумма первых
40 членов этой арифметической прогрессии.

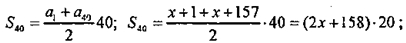
(2х+158)20 = 3200; 2х+158 = 160; 2х = 2; х = 1.
Ответ: 1.

6.29(2) (х+248)+(x+243)+(х+238)+…+(x+3) = 6225;
x+248, x+243, x+3 – арифметическая прогрессия, d = а₂-а₁ = -5; а₃-a₂ = -5.
Левая часть уравнения – сумма членов арифметической прогрессии, в
которой a₁ = х + 248: d = -5; an = a₁+d(n-1); x+3 = x+248-5(n-1);
-5(n-t) = -245; n = 50;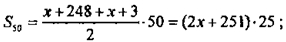
(2x+251)∙25 = 6225; 2х+251 = 249; 2х = -2; x = -1.
Ответ: -1,