Постройте отрезок §9 №10 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Даны пересекающиеся прямые и точка, не лежащая на этих прямых. Постройте отрезок с концами на данных прямых и серединой в данной точке.

1 ответ

ответы

Елизавета Мирошина

Пожаловаться

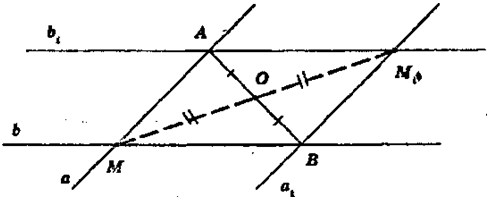
Пусть М - точка пересечения прямых а и b.
Построение:
1) Построим М1, симметричную М относительно точки О.
Через М1 проводим прямые а1 ‖ а и b1 ‖ b.
1) Точку пересечения прямых а и b1 обозначим А, а точку пересечения прямых b и а1 обозначим В.
Докажем, что АВ — искомый отрезок.
Стороны четырехугольника МАМ1В попарно параллельны, так как а ‖ а1, b ‖ b1, а значит, МАМ1В — параллелограмм.
Точка О — середина диагонали ММ1, так как М и M1 - симметричны относительно точки О.
Так как диагонали параллелограмма в точке пересечения делятся пополам, то диагональ АВ содержит точку О, которая является серединой АВ. Так что искомый отрезок - это АВ.