Помогите с решением задачи §9№17. Докажите, что ...Погорелов ГДЗ 11 класс геометрия.

Я думаю, что решение задачи §9№17 — вот это:
Решение. Пусть АА', ВВ', СС' — медианы данного треугольника
АВС. Тогда точки А', В' ,С ', являются по определению серединами его сторон. Значит:

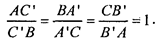
Поэтому произведение этих отношений также равно 1. По теореме Чевы (обратное утверждение) отсюда следует, что медианы треугольника пересекаются в
одной точке.
Замечание. Можно доказать, что теорема Чевы имеет место и в
том случае, когда некоторые из точек А', В', С' лежат не на самих
сторонах, а на их продолжениях. Но при этом надо учитывать, что
прямые АА', ВВ', СС' могут быть и параллельными, т.е. могут «пере-
секаться в бесконечно удаленной точке».