Помогите §9 №37 ГДЗ Геометрия 7-9 класс Погорелов А.В.

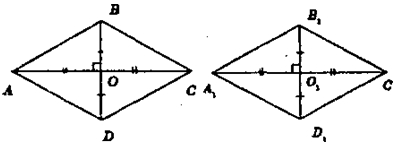
Пусть в ромбах ABCD и A1B1C1 равны диагонали АС и А С BD и B1D1. Пусть диагонали ромбов ABCD и A1B1C1D1 пересекаются в точках О и O1 соответственно.
Рассмотрим ΔАОВ и ΔA1O1B1:
∠AOB = ∠A1O1B1 так как диагонали ромба перпендикулярны,
АО = А1О1, ВО = B1O1, так как диагонали ромба в точке пересечения делятся пополам и по условию диагонали АС и А1С1 BD и B1D1 равны;
ΔАОВ = ΔA1O1B1 по двум сторонам и углу между ними, следовательно АВ = A1B1.
Так как в ромбе все стороны равны, то АВ = ВС = CD = AD = = A1B1 = B1C1 = C1D1 = A1D1.
Рассмотрим Δ ABC и ΔA1B1C1:
AB = A1B1; BC = B1C1 и AC = A1C1 (по условию), ΔABC = = ΔA1B1C1 по трем сторонам, значит, ∠ABC = ∠A1B1C1.
В задаче № 36* § 9 было доказано, что если две стороны и угол между ними одного параллелограмма соответственно равны двум сторонам и углу между ними другого параллелограмма, то такие параллелограммы равны.
В ромбах ABCD и A1B1C1D1 АВ = A1B1, ВС = В1С1 ∠ABC = = ∠A1B1C1, значит, эти ромбы равны.