Нужно доказать № 953 ГДЗ Геометрия 9 класс Атанасян Л.С.

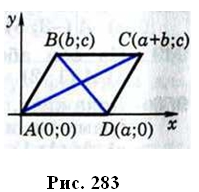
Пусть ABCD — данный параллелограмм. Введём прямоугольную систему координат так, как показано на рисунке 283. Если AD = BC = a, а точка В имеет координаты (b; с), то точка D имеет координаты (а; 0), а точка С — координаты (а + b; с). Используя формулу расстояния между двумя точками, находим:

АВ² = b² + с², AD² = а², АС2 = (а + b)² + с², BD² = (а - b)² + с². Отсюда получаем:
АВ2 + ВС² + CD² + DA² = 2 (АВ² + AD²) = 2 (а² + b² + с²),
АС² + BD² = (а + b)² + с² + (а - b)² + с² = 2 (а² + b² + с²).
Таким образом,
АВ² + ВС² + CD² + DA² = АС² +BD², что и требовалось доказать.