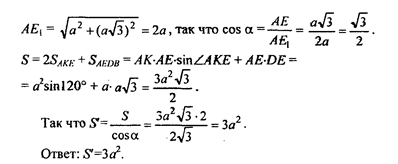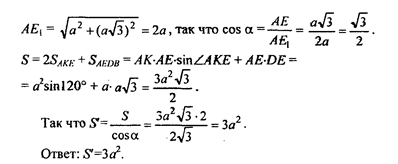Необходимо решить задание №14 Геометрия 11 класс Погорелов. Найти площадь построенного сечения

Ответ на задачу №14
Данное сечение проходит через основание АВ и E₁D₁. Обозначим точку пересечения прямых АВ и DC точка F. Тогда F принадлежит плоскости сечения, а также плоскости CC₁D₁D. Так что проведем прямую D₁F, которая пересечет ребро CC₁ в некоторой точке X.

 
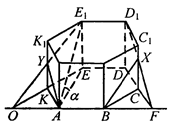
Далее, продолжим прямые ЕК и АВ до их пересечения в точке О.
Эта точка принадлежит плоскости сечения, а также грани КК₁Е₁Е.
Тогда проведем прямую ОЕ₁, которая пересечет ребро КК₁ в неко-
торой точке Y.
Шестиугольник ABXD₁E₁Y — искомое сечение. Найдем его пло-
щадь по формуле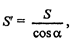 
где S — площадь основания призмы, а α — угол, который образует данное сечение с плоскостью основания. Так как ЕА┴АВ. то и Е₁А┴АВ (по теореме о трех перпендикуляpax). Так что ∟ΕΑΕ₁= α. Далее, ΕΕ₁ = а, и 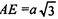(по теореме косинусов из ∆AЕК), Далее, по теореме Пифагора: