Необходимо решить задачу № 8 Постройте сечение четырехугольной призмы плоскостью Погорелов ГДЗ 11 класс Геометрия
Решение задачи №8 :
Пусть К, М и N - данные точки.
Возможны три случая:
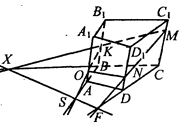
1) Точки К, Μ, N расположены так, что
MN || DC и КМ || MN. Тогда плоскость, про-
ходящая через точки К, М и N параллельна плоскости грани ABCD, т.к. две пересекающие прямые КМ и MN
параллельны грани ABCD. Проведем прямую ON || AD. Тогда она
будет принадлежать плоскости сечения. Так как иначе она пересе-
кала бы и грань ABCD, то есть и AD, что неверно.
Тогда четырехугольник KMNO - искомое сечение.
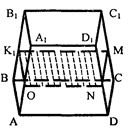
2) Точки К, Μ, N располагаются
так, что KM || ВС, но MN не парал-
лельно DC. Тогда через точки М и N
проведем прямую а, которая пересе-
кает прямую DC в некоторой точке S.
Тогда S принадлежит сечению. Че-
рез точку S проведем прямую b || КМ.
Тогда b принадлежит сечению и b|| ВС,
т.к. b || КМ и КМ || ВС. Тогда АВ пере-
секает прямую b в некоторой точке X.
Тогда X принадлежит сечению. А так-
же можно соединить точи К и Х отрезком, который пересечет А1А в
некоторой точке О. Тогда точка О тоже принадлежит сечению. А
значит, четырехугольник OKMN—это искомое сечение.
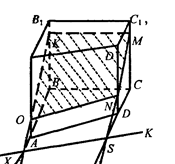
Общий случай:
3) Когда точки К, М, N распо-
лагаются так, что MN не парал-
лельно DC и КМ не параллельно
MN. Тогда прямая MN пересечет
прямую DC в некоторой точке F,
прямая МК пересечет прямую ВС в
некоторой точке X Точки X и F
принадлежат плоскости ABCD, а
также искомому сечению, значит, плоскость ABCD и сечение пере-
секаются по прямой XF. Тогда прямая АВ, или прямая AD, или обе
эти прямых пересекают прямую XF. Допустим АВ пересекает XF в
точке S. Тогда точка S принадлежит и плоскости АА1В1В, а также сечению. Проведем прямую SK. Она пересечет ребро АА1 в точке О.
Так что MNOK - искомое сечение.
