Не могу додуматься, как решить, задача §9№55. Постройте квадрат. ГДЗ 11 класс Погорелов геометрия

Не могу додуматься, как решить, задача §9№55.
Постройте квадрат, стороны которого проходят через четыре заданные точки А, В, С, D.

1 ответ

ответы

Мария Клищенкова

Пожаловаться

Вот решение задачи §9№55
Допустим, что квадрат построен . Повернем отрезок DB около точки D на угол 90°. Получим отрезок DB' А теперь перенесем его параллельно так, чтобы точка D совместилась с точкой А. При этом точка B' попадет в точку В' на стороне квадрата,

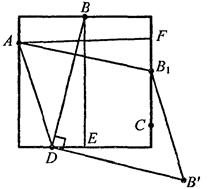
которая проходит через точку С (или на продолжение этой сторо-
ны). Это следует из равенства прямоугольных треугольников
BED и AFB1 (у них гипотенузы BD и АВ1 равны по построению, а
катеты BE и AF равны стороне квадрата).
Построив точку B1, проводим прямую СВ1, на которой лежит
сторона квадрата. Далее проводим через точку А прямую, параллель-ную СВ1, и через точки В и D прямые, перпендикулярные этой пря-
мой. Искомый квадрат построен.