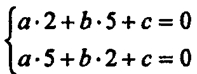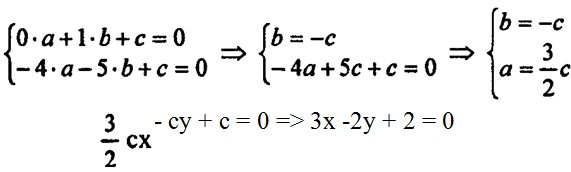Напишите № 972 ГДЗ Геометрия 9 класс Атанасян Л.С.

Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2); б) С (2; 5)иD (5; 2); в) М (0; 1) и N (-4; -5).
Решение
а) Уравнение прямой АВ имеет вид ах + by + с = 0. Так как точки А и В лежат на прямой АВ, то их координаты удовлетворяют этому уравнению:
а • 1 + b • (-1) + с = 0, а • (-3) + b • 2 + с = 0,
или а - b + с = 0, -За + 2b + с = 0.
Из этих уравнений выразим коэффициенты а и b через с: а = 3с, b = 4с. Подставив эти значения в уравнение прямой, получим 3сх + 4су + с = 0. При любом с≠ 0 это уравнение является уравнением прямой АВ. Сократив на с, запишем искомое уравнение в виде 3х + 4у + 1 = 0.