Надо доказать §9 №35 ГДЗ Геометрия 7-9 класс Погорелов А.В.

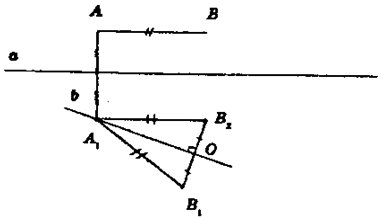
Пусть длины отрезков АВ и A1B1 равны.
Подвергнем отрезок преобразованию симметрии относительно прямой а, перпендикулярной отрезку АА1 и проходящей через его середину. Получим отрезок A1B2 если В1 и В2 совпадают, то значит, АВ и А1В2 равны, если не совпадают, то подвергнем отрезок А1В2 преобразованию симметрии относительно прямой b, содержащей биссектрису угла В2A1В1. Так как ΔВ2А1B1 является равнобедренным, то его биссектриса является серединным перпендикуляром к В1В2 и, значит, при симметрии относительно прямой b точка В2 перейдет в точку B1.
Таким образом, отрезок АВ в результате рассмотренного движения перешел в отрезок A1B1.

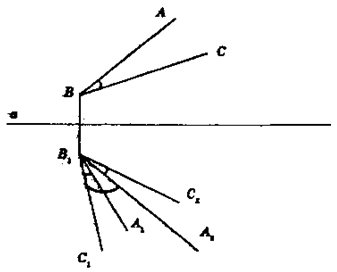
Пусть градусные меры углов АВС и A1B1C1 равны.
 В результате симметрии относительно прямой а, являющейся серединным перпендикуляром к ВВ1, и поворота вокруг В1 на угол А2В1С1 угол АВС совместится с углом A1B1C1. Что и требовалось доказать.