Как решить №73. Найдите высоту. ГДЗ Геометрия Погорелов 11класс

Дополним усеченную пирамиду до полной. Так как в правильной пирамиде высота проходит через центр окружно-
сти, вписанной в основание, то О и Ο₁ — центры окружностей, вписанных в АВС и А₁В₁С₁.

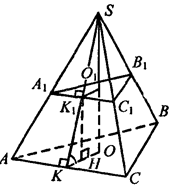
Проведем SK┴AC, а значит, и SK₁┴A₁C₁. Тогда по теореме о трех пер-
пендикулярах ОК┴АС и ОК₁┴А₁С₁. Значит, ОК и O₁К₁ — радиусы окружностей, вписанных в правильные треугольники АВС и А₁B₁C₁


Далее, проведем Κ₁Η┴ΚΟ. Тогда Κ₁Ο₁ΟΗ — прямоугольник, значит, К₁Н=OO₁
Так как ∟Κ₁ΚΗ является линейным углом двугранного угла ме-
жду основанием и боковой гранью, то ∟Κ₁ΚΗ =60° (по условию).
Тогда в ∆Κ₁ΚΗ: Κ₁Η=ΚΗ· tg∟K₁KH = √3 KH.