Как решается задача §9№39. Найдите объем пирамиды. Геометрия Погорелов 11 Класс ГДЗ

Задача §9№39 решается так:

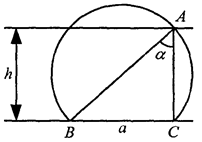
Пусть сторона BС искомого треугольника АВС равна а,противолежащий ей угол А равен α, а высота, проведенная из вершины этого угла, равна А. Допустим, задача решена . Тогда вершина А принадлежит геометрическому месту точек, из которых отрезок ВС виден под углом а и которые расположены
по одну сторону от прямой BС, т.е. дуге окружности с концами в
точках B и С. Кроме того, она лежит на прямой, параллельной
прямой BС, т.е. дуге окружности с концами в точках B и С. Кро-
ме того, она лежит на прямой, параллельной прямой ВС и от-
стоящей от нее на расстоянии h. Поэтому вершина А является их
точкой пересечения.
Для решения задачи достоточно построить прямую, параллель-
ную АС и отстоящую от нее на А, и воспользоваться решением за-
дачи 35 из п. 87. Задача может иметь два решения, одно решение
или ни одного. Это зависит от числа точек пересечения прямой,
параллельной прямой BС, с дугой окружности с концами в точках
B и С.