Как построить отрезок §9 №24 ГДЗ Геометрия 7-9 класс Погорелов А.В.
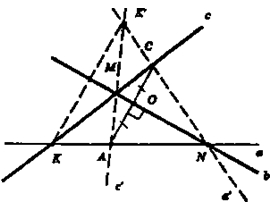
Пусть прямые а и с пересекаются в точке К, b и с в точке М, а и b в точке N.
Предположим, что задача решена и отрезок АС с концами на прямых а и с перпендикулярен b и в точке пересечения с прямой b делится пополам. Точки А и С симметричны относительно прямой b.
Рассмотрим симметрию относительно прямой b. При этом прямая b отобразится на b;
точка N — на N (как лежащая на прямой b); точка М — на М (как лежащая на прямой b); точка К — на К'; точка А — на С.
Следовательно прямая с отобразится на прямую с', проходящую через К', M, А, так как с проходит через К, М, С;
прямая а — на прямую а', проходящую через точки К', N, С, так как прямая а проходит через точки К, N, А.
Через точку А проходят прямые а и с', через точку С — прямые с и а'.
Построение.
1. Строим точку К', симметричную К относительно прямой b.
2. Через точки К' и М проводим прямую с', симметричную прямой с так как К' симметрична К, а М симметрична М, относительно прямой b.
3. Через точки К' и N проводим прямую а', симметричную прямой а, так как К' симметрична К, а N - симметрична N, относительно прямой b.
4. Обозначим точку пересечения прямых с и а' точкой С, а точку пересечения прямых а и с' обозначим А. Построим отрезок АС.
Докажем, что АС — искомый отрезок.
По построению прямые а и а', с и с' симметричны относительно прямой b, А — точка пересечения прямых а и с', значит, симметричная ей точка это точка пересечения прямых а' и с, то есть точка
С. Значит точки А и С симметричны относительно прямой b, значит, АС — искомый отрезок.
Исследуем, всегда ли задача имеет решения и сколько решений возможно.
Задача не будет иметь решение, если нельзя построить точки А и С, то есть, если прямые а и с' или с и а' не пересекаются, то есть, если
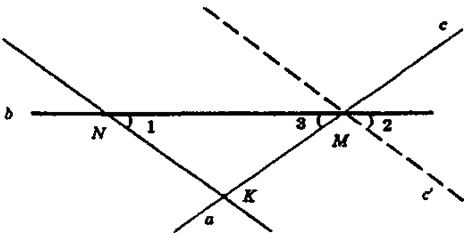
Прямые а и с' параллельны тогда и только тогда, когда ∠1 = Z2 (соответствующие углы при пересечении прямых а и с секущей b) Но прямая С симметрична С, поэтому образует с прямой b угол 3, равный углу между С и В, то есть углу 2. Так что ∠1 = ∠2, ∠2 = ∠3, то есть ∠1 = ∠3 Значит, ΔMKN — равнобедренный.
То есть если при попарном пересечении прямых а, b, с получится равнобедренный ΔMNK с основанием MN, лежащим на прямой b, то задача не будет иметь решения.
Далее заметим, что при любом другом способе построения отрезок С'А', удовлетворяющий условию задачи, должен быть симметричен относительно прямой b, а значит, его концы должны лежать как на прямых а и с, так и на симметричных прямых а' и с1, то есть точки А' и С, должны совпадать с построенными точками А и
С.
Значит, при любом способе построения задача будет иметь единственное решение, если точки пересечения прямых не являются вершинами равнобедренного треугольника с основанием, лежащим на прямой b, в противном случае задача решений не имеет.
