Хело! Помогете решить неравенства? Раздел II. № 3.35. ГДЗ Алгебра 9 класс ОГЭ Кузнецова.

3.35(1) (x + 1-√3)(x- √6 + 2) > 0. Запишем неравенство в виде:
(x - (√3 - 1))(x - (√6 - 2)) > 0 . Тогда (√3 - 1) и (√6 - 2) - корни
квадратного трехчлена, ветви графика которого направлены вверх,
следовательно, нужные нам значения х располагаются слева от
меньшего корня и справа от большего. Выясним, что больше √3 - 1
или √6 - 2. √3 - 1 >0; √6 - 2 > 0,
(√3-1)2 = 4-2√3 = 2(2-√3), (√6-2)2 = 10-4√6 = 2(5-2√6).
Сравним 2-√3 и 5-2√6;
1)       1,7 < √3 < 1,8; -1,8 < -√3 < -1,7; 0,2 <2-√3 < 0,3;
2)       2,4 < √6 < 2,5; 4,8 < 2√6 <5; -5 < -2√6 < -4,8.
0 < 5-2√6 < 0,2 . Таким образом, 5 - 2√6 < 0,2 < 2-√3 .
Следовательно 5 - 2√6 < 2 - √3 и √6 - 2 < √3 - 1.
 
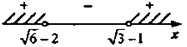
Ответ: х < √6 - 2; х >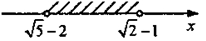 √3 - 1.
 
 
3.35(2) (x-√5+2)(х + 1-√2) < 0
Запишем неравенство в виде: (x-(√5-2))(x-(√2-l))<0 То-
гда (√5-2) и (√2-1) - корни квадратного трехчлена, ветви гра-
фика которого направлены вверх, следовательно нужные нам значе-
ния х расположены между его корнями.
Выясним, как расположены корни этого трехчлена. Сравним,
что больше √5-2 или √2-1. Имеем: 0,23<√-2<0,24;
0,41 <√2-1 <0,42.
Следовательно √2-1>√5 - 2. √5-2<х<√2-1
 
Ответ: √5-2<х<√2-1.