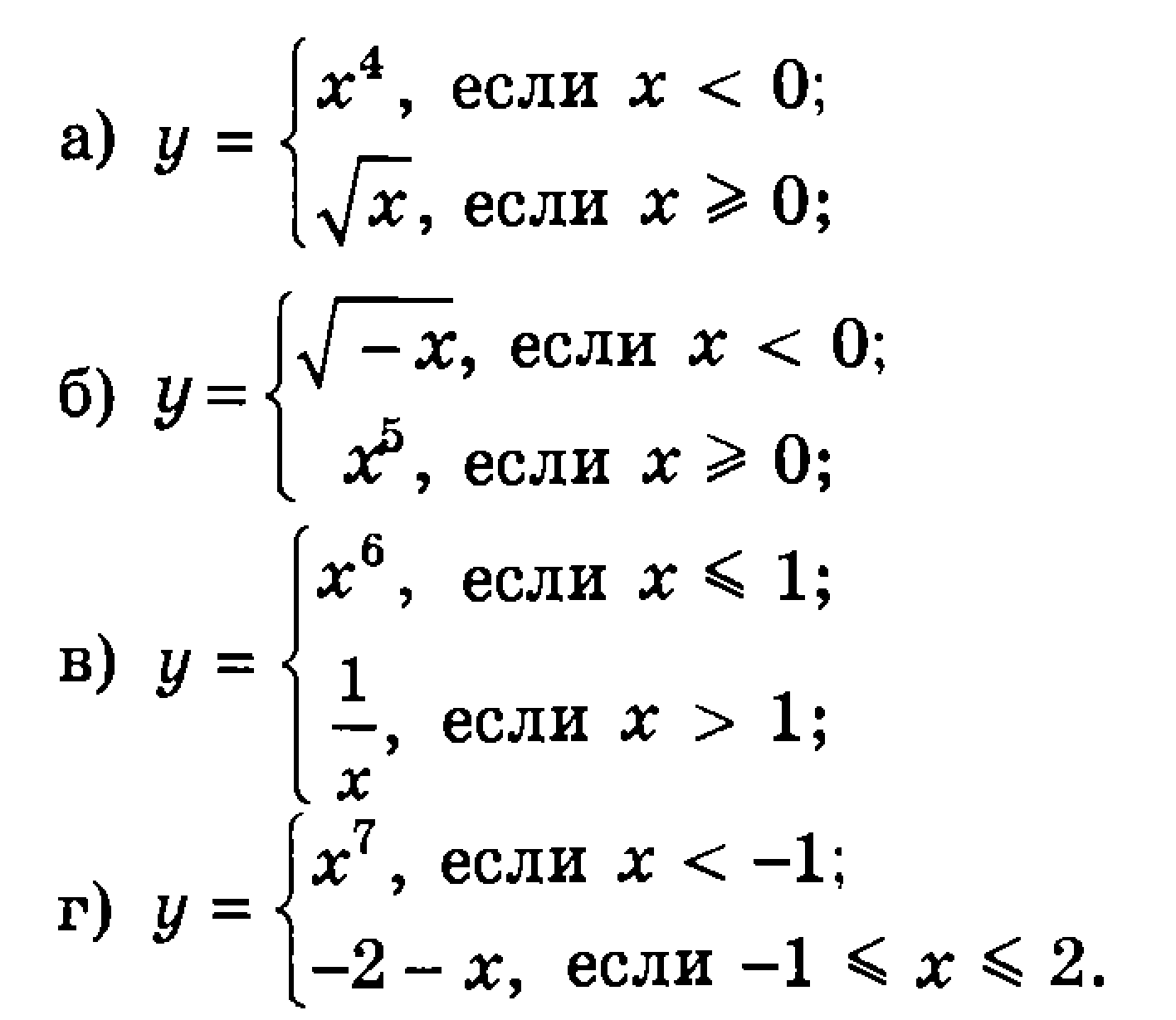Хело! Как прочитать эти графики? № 12.19 Алгебра 9 класс Мордкович.

Постройте и прочитайте график функции:

1 ответ

ответы

Ирина Моркела

Пожаловаться

1) D(f) = (-∞; +∞); 2) Ни четная, ни нечетная. 3) На (-∞; 0] убывает. Возрастает на [0; +∞). 4) Не ограничена сверху, ограничена снизу. 5) y_min = 0; y_max – не существует. 6) Непрерывна. 7) Е(f) = [0; +∞). 8) На (-∞; 0] выпукла вниз. На [0; +∞) выпукла вверх.

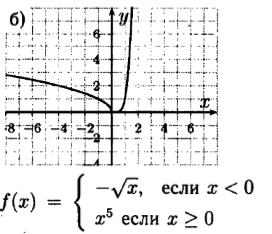
1) D(f) = [0; +∞); 2) Ни четная, ни нечетная. 3) Возрастает. 4) Не ограничена сверху, ограничена снизу. 5) y_min = 0; y_max – не существует. 6) Непрерывна на области определения. 7) Е(f) = [0; +∞). 8) Выпукла вверх на (-∞; 0], выпукла вниз на [0; +∞).

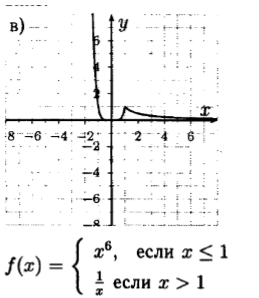
1) D(f) = (-∞; +∞). 2) Ни четная, ни нечетная. 3) Возрастает на [0; 1]. Убывает на (-∞; 0] и на [1; +∞). 4) Не ограничена сверху, ограничена снизу. 5) y_min = 0; y_max – не существует. 6) Непрерывна. 7) Е(f) = [0; +∞). 8) На (-∞; 1] и на [0; +∞) выпукла вниз.

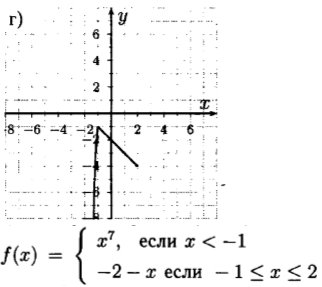
1) D(f) = (-∞; 2]. 2) Ни четная, ни нечетная. 3) Возрастает на (-∞; 1]. Убывает на [-1; 2]. 4) Не ограничена сверху, ограничена снизу. 5) y_max = -1. 6) Непрерывна. 7) Е(f) = (-∞; -1]. 8) Выпукла вверх на (-∞; -1]. На [-1; 2] можно считать выпуклой как вверх, так и вниз.