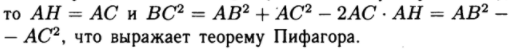ГДЗ по геометрии Атанасян 8 класс. Гл.VI №532. Докажите, что если...

Необходимо решить задание, нужна помощь Гл.VI №532.
В треугольнике АВС проведена высота ВН. Докажите, что если:
а) угол А острый, то ВС2 = АВ2 + АС2 - 2АС • АН;
б) угол А тупой, то ВС2 = АВ2 + АС2 + 2АС • АН.

1 ответ

ответы

Ольга К

Пожаловаться

Привет, я решила задачу Гл.VI №532, помогаю

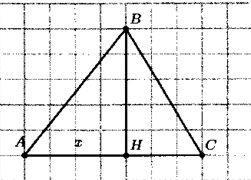
В треугольнике АВС с высотой ВН зададим. Высота
ВН — общий катет двух прямоугольных треугольников
АВН и ВСН.
а) Для ΔАВН имеем ВН² = АВ²-АН². Для ΔВНС
имеем ВН² = ВС² - НС², откуда АВ² - АН² = ВС² - НС²
→ ВС² = АВ² - АН² + НС² = АВ² + (АС - АН)² - АН² =
= АВ² + АС² - 2АС · АН + АН² - АН² =
= АВ² + АС² — 2АС· АН. Что и требовалось доказать.
В случае если угол С = 90о (Треугольник ABC - прямоугольный),

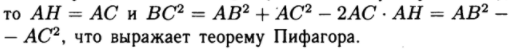
б) Для ΔАВH имеем ВН² = АВ²-АН².
Для ΔВНС имеем ВН² = ВС² - НС², откуда АВ² - АН² = ВС² -
- НС² → ВС² = АВ² - АН² + НС² = АВ² + (АС +
+ АН)² - АН² = АВ² + АС² + 2АС · АН + АН² - АН² =
= АВ² + АС² + 2АС · АН. Что и требовалось доказать