ГДЗ по геометрии Атанасян 8 класс. Гл.V №389. Докажите, что трапеция равнобедренная...

Вот докозательство для задачи Гл.V №389:
Пусть в трапеции АВСD с основаниями АD и ВС, АD > ВС.
а)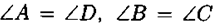 
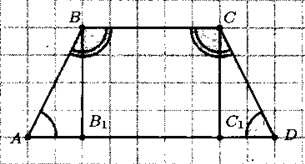
На сторону АВ из точек В и С опустим перпендикуляры ВВ₁  и CC₁, ΔАВВ₁ = ΔСDС₁ по катету и острому углу (так как ВВ₁ = СС₁ (ВСС₁В₁ — прямоугольник), .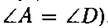
Следовательно,  АВ = СD, значит АВСD — равнобедренная трапеция.
 
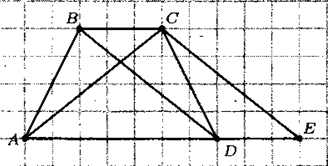
б) АС = ВD. Проведем прямую СЕ||ВD, такую что точка Е лежит на прямой АD. Так как ВС||DЕ и ВD||СЕ, то ВСЕD — параллелограмм. Значит СЕ = ВD = АС, ΔАСЕ — равнобедренный, и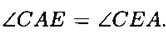  
Так как СЕ||ВD, то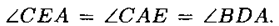 
Следовательно ΔАСD = ΔАВD по двум сторонам и углу между ними,
значит АВ = СD, и АВСD — равнобедренная трапеция.