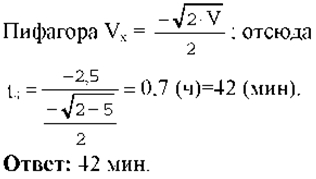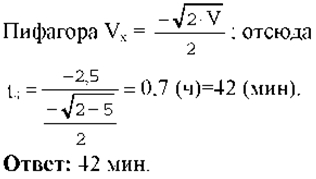Где окажется группа Упражнение 2 № 1 ГДЗ Физика 9 класс Кикоин И.К.

За начало отсчета координат примем точку отправления группы туристов. Оси координат направим вдоль сторон света.
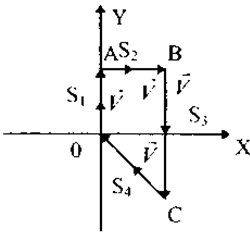
На рис. 1 изобразим траекторию движения туристов. Весь путь разобьем на четыре участка, на которых движение группы определяете: векторами перемещения S1,S2 ,S3,S4 соответственно в направлении на север, восток, юг и обратно в исходную точку. На каждом из них укажем скорость движения V и отметим время движения t1, t2, t3, t4.
Дано: t1=1 ч t2=0,5 ч t3=1,5 ч V=5 км/ч S4 - ?
t4 - ?

Определим длину перемещения группы на участках ОА; АВ; ВС:
S1V ∙ t = 5∙1 = 5 км; S2 = 2,5 км; S3 = 7,5 км
Определим координаты группы в (∙) А:
xa=xo+Sxi
yA=yo+Sy1
Т.к. S направлен вдоль оси Y, следовательно хА=0+0=0; yA=0+S1 =0+5=5 км.
Координаты группы, в (∙) В:
xB=xA+Sx2
yB=yA+Sy2
Т.к. S2 направлен вдоль оси X, следовательно
xb=0+ |S2| =0+2,5 км=2,5 км;
yb=ya+0= 5 км+0 км=5 км.
Аналогичным путем определяем координаты группы в точке С:
хc=2,5 км, уc=—1,5 км.
Длину вектора S4 определим по теореме Пифагора:

Т.к. точка С находится в IV четверти координатной плоскости и лежит на прямой являющейся биссектрисой угла YOX (т.к. |ус| = |yC|),
то можно сделать вывод, что преодолев три участка ОА, АВ, ВС, группа оказалась на расстоянии 3,5 км к юго-востоку от исходного пункта. Время, требуемое на возвращение в