Докажите § 60 № 4 ГДЗ Физика 10 класс Громов С.В.

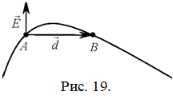
Рассмотрим две близкие точки А и В
на эквипотенциальной поверхности (см. рис.
19). Потенциалы в этих точках φ(А) и φ(В)
равны, т.е. φ(А) - φ(В) = 0. Пусть малое рас-
стояние между точками А и В равно d͞. То -
гда φ(А) - φ(В) = ͞E ∙ ͞d (Малость d требуется, чтобы было можно ис-
пользовать эту формулу, справедливую для однородного поля. При
этом мы считаем, что на расстоянии d поле меняется не сильно и может
считаться однородным). Значит, E ∙ ͞d = 0 . Значение этого скалярного произведения равно нулю, если, либо E = 0, либо d = 0, либо ͞E перпендикулярно ͞d . Два первых условия не выполнены, значит, выполнено третье условие, т.е. ͞E перпендикулярно ͞d . Учитывая, что ͞d мало,
d — касательная к эквипотенциальной поверхности. Отсюда заключаем, что напряженность перпендикулярна эквипотенциальной поверхности, т. е. силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям.