Алимов 452 доказать!

Без ограничения общности можем считать, что х2 > х1.  Предположим, что
у2 > у1. Заметим, что отрезок — часть прямой, причём коэффициент k > 0. Предположим, что утверждение неверно. Пусть, к примеру,

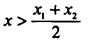
=> 2x > х1 + х2. Из этого следует, что 2у > у1 + у2,
т.к. отрезок —- это часть прямой и  k > 0.
Запишем условие того, что С — середина отрезка.

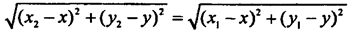
х₂² - 2х²х + x² + у₂² - 2у²у + y² = х₁ ² - 2х¹х + x² + у₁² - 2у¹ у + y² =>
х₂² - х₁² - 2х(х₂ -х₁) + у₂² - у₁² - 2у(у₂ - у ) = 0  =>
(х₂ - x₁ )+ (х₂ + x₁ - 2х) + (у₂ -у₁)(у₂ -у₁ - 2у) = 0 — противоречие, т.к.
(х₂-х₁) > 0, (х2 + x₁ - 2x) < 0, (у₂-у₁) > 0, (у ₂-у₁- 2у) < 0, а следовательно,
(х₂ - х₁)(х₂ + x₁- 2х) + (у₂-у₁)(у₂-у₁- 2у) < 0.
 
Значит, предположение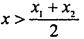 
- неверно.
Аналогично доказывается ложность предположения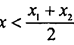 
Следовательно,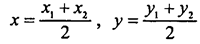 
 Случай  y₂ <  y₁ сводится к предыдущему, случай когда  x₁ = x₂ или_y₁ = y₂ очевиден.