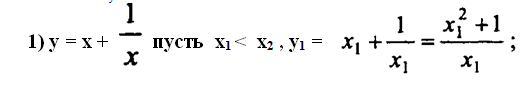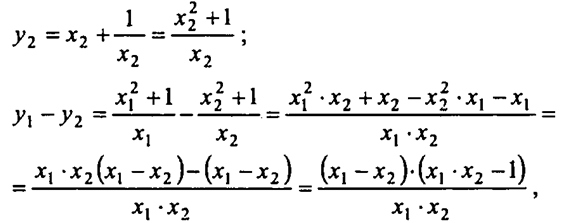Алгебра. 9 класс. Алимов Ш. А. Параграф 13. Упражнение №170. Провести доказательства с функциями.

Приветик, смотри ответ ниже.


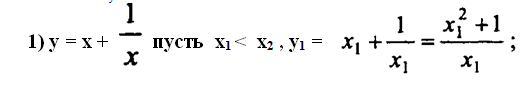
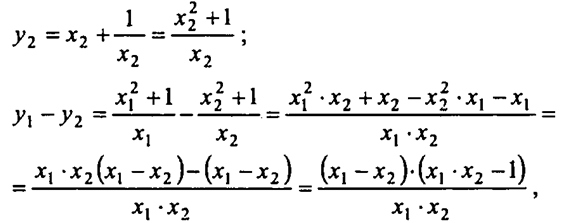
При  х₁, х₂ > 0, имеем х₁ -х₂ < 0,  х₁ ∙ х₂ > 0, х₁ ∙ х₂ - 1 < 0
Тогда 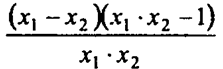> 0, поэтому  у₁ > у₂
Тогда т.к.  х₁ <  x₂,  но  у₁ > у₂, функция убывает на интервале 0 < х < 1.
2)
у =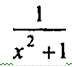

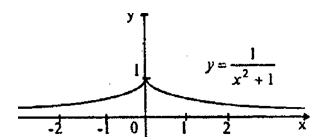
у   возрастает при   х ∈ (∞ ; 0];                          
у   убывает при   х ∈ [0; + ∞).
3)      у = х³ - х.
Пусть х₁<x₂  и  x₁, х₂ < = - 1, значит y₁ = х³ - 3х,; y₂ = x² - 3x²
Тогда y₁ - y₂ = x₁³ - 3x₁ - 3x₂ = (х₁³ - x₂³) - 3(x₁ - x₂ ) =
= (х₁ - x₂ )(x₁² + x₁x₂ + x₂² ) - 3(x₁ - x₂ ) = (х₁ - x₂ )(x₁² + x₁x₂ + x₂² - 3) < 0
При   х₁ <= - 1,  x₂ <= - 1, имеем x₁² + x₁x₂ + x₂²  >= 3,
поэтому x12 + x1x2 + x22 - 3 >= 0, значит, т.к. х1<x2   и  y1 < y2, то у возрастает при х <=  - 1, и х >= 1 и убывает при   - 1  х  1.
4) у = х - 2 ;  пусть х1 < х2 и х1, х2 >= 1, тогда

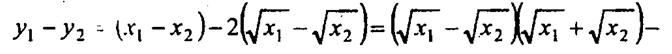
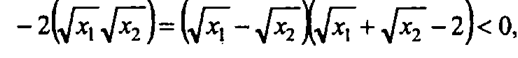при х ₁ >= 1,
х2 >= 1, имеем :     1 >= 1,  2 >= 1, значит  1 +  2 >= 2, поэтому, т.к. х1<x2  и  у1<у2 , то    у   возрастает при  х >= 1, и убывает при 0  х  1.