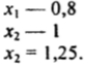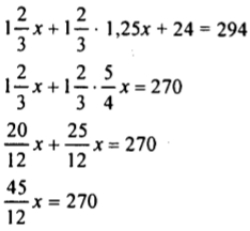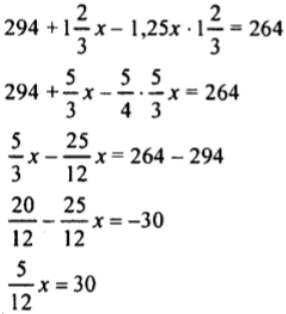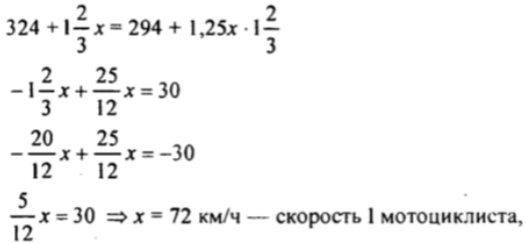№ 201 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите решить задачи про скорость.
Чем похожи и чем отличаются задачи? Реши их и сопоставь решения.
1) Из двух городов, расстояние между которыми 294 км, одновременно навстречу друг другу выехали два мотоциклиста. Через 1 ч 40 мин расстояние между ними стало равно 24 км. Скорость первого мотоциклиста составляет 80% скорости второго. С какой скоростью они ехали?
2) Из двух городов, расстояние между которыми 294 км, одновременно в одном направлении выехали два мотоциклиста. Через 1 ч 40 мин расстояние между ними стало равно 264 км. Скорость первого мотоциклиста составляет 80% скорости второго. С какой скоростью они ехали?
3) Из двух городов, расстояние между которыми 294 км, одновременно в противоположных направлениях выехали два мотоциклиста. Через 
ч расстояние между ними стало равно 564 км. Скорость первого мотоциклиста составляет 80% скорости второго. С какой скоростью они ехали?
4) Из двух городов, расстояние между которыми 294 км, одновременно в одном направлении выехали два мотоциклиста. Через 1 ч 40 мин расстояние между ними стало равно 324 км. Скорость первого мотоциклиста составляет 80% скорости второго. С какой скоростью они ехали?
1)
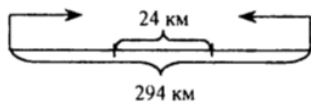
Пусть х км/ч - скорость I мотоциклиста, зная, что она составляет 80% скорости II мотоциклиста, найдем:
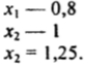
Значит, скорость II мотоциклиста - 1,25х км/ч.
Зная, что через l ч 40 мин расстояние между мотоциклистами стало 24 км, составим уравнение:
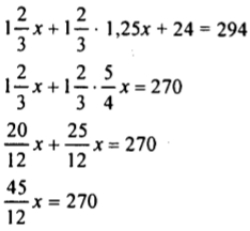
х = 72 (км/ч) - скорость 1 мотоциклиста,
1,25 · 72 = 90 км/ч - скорость 11 мотоциклиста.
Ответ: 90; 71 км/ч.
2)
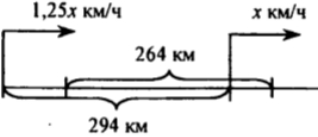
Пусть х км/ч - скорость I мотоциклиста, тогда 1,25х км/ч - скорость II.
Зная, что через 1 ч 40 мин расстояние между ними стало 264 км и данные задачи, составим уравнение:
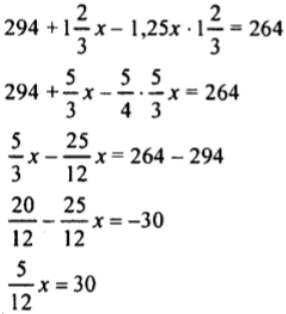
х = 72 км/ч
1,25х = 1,25 · 72 = 90 км/ч - скорость II мотоциклиста.
Ответ: 72; 90 км/ч.
3)
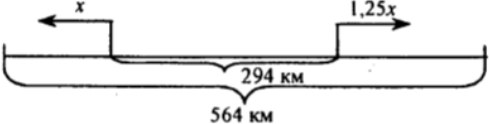
Пусть х км/ч - скорость I мотоциклиста. 1,25х км/ч - скорость II мотоциклиста; зная, что через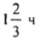 
расстояние между ними стало 564 км, а первоначальное расстояние 294 км, составим и решим уравнение:
1,25х = 90 км/ч -скорость II мотоциклиста.
Ответ: 72 км/ч, 90 км/ч.
4)
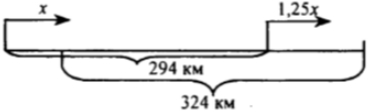
Пусть х км/ч -скорость 1 мотоциклиста, 1,25х -скорость II. Зная, что расстояние между пунктами 294 км, а через 1 ч 40 ми н оно стало 324 км, составим уравнение:
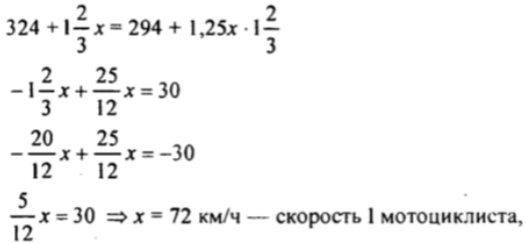
1,25х = 90 км/ч -скорость II мотоциклиста.
Ответ: 72 км/ч, 90 км/ч.
Схожесть задач заключается в тематике, в условии, расстоянии между пунктами, времен и в пути. При решении ответы получились одинаковыми. Различия заключаются в направлении движения мотоциклистов, в расстоянии, которое в зависимости от направления, разное.
