№ 196 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Чем похожи и чем отличаются задачи?

1)

Пусть х км/ч - скорость 1-го поезда, тогда х + 12 км/ч - скорость второго.
Зная, что расстояние между городами 490 км, составим уравнение:
3,5 · х + 3,5(х + 12) = 490
3,5(х + х + 12) = 490
2х + 12 = 140; 2х = 128
х = 64
64 км/ч - скорость 1-го поезда,
(64 + 12) км/ч или 76 км/ч -скорость 2-го поезда.
Ответ: 64, 76 км/ч.
 
2) Пусть х км/ч - скорость 1 поезда, х - 12 км/ч - скорость II поезда. Зная, что 1 поезд вышел на 1 час раньше первого и они встретились через 3,5 ч, составим уравнение:
4,5х + 3,5(х - 12) = 490
4,5х + 3,5х - 42 = 490
8х = 532
х = 66,5 км/ч - скорость I поезда,
54,5 км/ч -скорость 11 поезда.         ·
Ответ: 66,5 км/ч; 54,5 км/ч.
 
3) 1,7η₂ = η₁

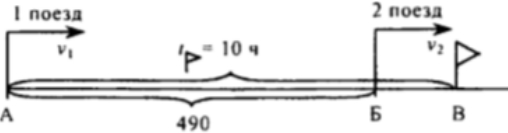
Пусть х - скорость II поезда, тогда 1,7х - скорость 1 поезда.
Зная, что расстояние между городами равно 490 км и I поезд нагонит второй через 10 ч, составим уравнение:
10 · 1,7х = 490 + 10х
17х - 10х = 490
7х = 490
х = 70 км/ч - скорость II поезда,
70 · 1,7 = 119 км/ч -скорость I поезда.
Ответ: 70 км/ч; 119 км/ч.
Сопоставив задачи, можно сделать вывод, что принцип решен и их одинаковый. 3-я задача отличается в условии, по решению она наиболее сложная.

Пиздабол, если x - скорость первого, тогда будет 4.5х..., а если x - скорость второго, тогда 3.5(х+12) а не 3.5(х-12)