№ 126 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите опровергнуть

Прочитай утверждения и опровергни их. Построй их отрицания.
1)    ∀ а ∊ R : а² > a (R- множество дробей);
2)     ∀ b ∊ N : b² + b + 1 - простое число;
3)     ∀ х, у ∊ N: (х + у)² = х² + у²;
5)     ∃ а, b ∊ N : (а + b)² = 5;
6)     ∃ c, d ∊ N : с² + d² = 6;
7) ∃ х, у ∊ N : х + у = 7 и ху =7;
4) ∀m, n Е N:
8) ∃ m, n, k ∊ N:

1 ответ

ответы

Соня Говорун

Пожаловаться

1) ∀ а: а2 > а. Неверно, например, для а = l .
2) ∀ b: b2 + b + 1 - простое число. Неверно, например, для b = 1/2.

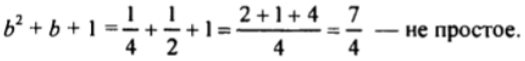
3) ∀ x, y, z ∈ N: (х + у)² = х² + у². Неверно, например, для х = 3, у = 5:
(3 + 5)² = 64; 3² + 5² = 43.
4) ∀ m, n ∈ N: m/n = n/m. Неверно, например, для m = 4, n = 10.
4/10 ≠ 10/4.
5) ∃ a, b ∈ N: (а + b)² = 5.
Из этого высказывания следует, что 2 < (а + b) < 3, но не существует натурального числа, удовлетворяющего этому условию. Значит, высказывание ложно.
6) ∃ с, d ∈ N: с² + d² = 6.
Воспользуемся методом перебора.
Если с = 1, d = 2, то с² + d² = 5; если d = 1, с = 2, то с2 + d2 = 5. Если с = 2, d = 2, то с² + d² = 8.
Очевидно, что предполагая с > 2 и d > 2, получим с² + d² > 8. Следовательно, не существует таких натуральных с и d, что с² + d² = 6, значит, высказывание ложно.
7) ∃ х, у ∈ N: х + у = 7 и ху = 7.
Число 7 - простое, т.е. может быть представлено только как произведение единицы на само себя. Но в таком случае не выполняется 1-ое условие, т.к. х + у = 8. Значит, высказывание ложно.
8) ∃ m, n ∈ N: m/n ≠ mk/nk.
Т.к. k ∈ N, то дробь mk/nk всегда можно представить в виде m/n, сократив и числитель, и знаменатель на k. Значит, предположение ложно.